什么问题

解决规模效率的问题, 基本思路是如果数量越多, 就让他的成本更低

举个例子:

我们店里有三种一次性商品: 纸杯, 手套, 口罩

商品的货架位置分别在 1 米(纸杯), 3 米(手套), 5 米(口罩)

而根据我们出货数量的统计发现

口罩每天能卖 100 个, 手套 20 个, 纸杯 10 个

这样我们算一下每天总共需要走多少米

1
2
3

100个口罩 * 5米(口罩货架的位置) + 20个手套 * 3米(手套货架的位置) + 10个纸杯 * 1米(纸杯货架的位置)

100 * 5 + 20 * 3 + 10 *1 = 570米

总觉得哪里不太对劲啊

为什么口罩购买的那么多, 却放在那么远的
而纸杯购买那么的那么少, 反而放的那么近

假如我们把纸杯和口罩的货架位置转换一下后再来看看

1
2
3

100个口罩 * 1米(口罩货架的位置) + 20个手套 * 3米(手套货架的位置) + 10个纸杯 * 5米(纸杯货架的位置)

100 * 1 + 20 * 3 + 10 *1 = 170米

看看, 只是的换了一下位置, 就比之前节省了 400 米.

编码是什么东西

所谓的编码, 是将我们想要传输的信息转为能够理解的信息格式

众所周知, 计算机识别二进制, 比如

000 => 哈
001 => 夫
010 => 曼
011 => 编
100 => 码

这样计算机是不是就能帮助我们传递信息了

传递哈夫曼编码四个字共需要 15 个比特

等长编码

每个编码的位数是一样长的就是等长编码

比如使用最广的ASCII码用 1 个字节编码

0000 0000 => a
0000 0001 => b
0000 0010 => c
0000 0011 => d

这样我传输 4 个字符, 就需要 32 个 bit, 感觉有点浪费啊, 前面的 0 光占坑不干活

有没有办法能节省下, 我们知道在传输速度不变的情况下, 传输总量越小, 消耗时间也越少

变长编码

比如, 我们用
0 => a
1 => b
01 => c
10 => d

总共就需要传输 6 个 bit, 等等, 等等, 不太对劲.

计算机怎么识别01代表c还是a和b呢, 貌似识别不出来啊.

既然这样, 那将有冲突的二进制去掉就可以了.

0 => a
11 => b
100 => c
101 => d

这样看来, 发送 4 个字符, 总要需要 9 个 bit

相比于等长编码的 32 个 bit, 我们节省了 23 个 bit,

字符的频率

大致的思路都理解了, 现在我们从一个实际的例子触发

假设我们传输一段信息, 为了方便, 我们拿英文来举例

Don't be afraid to shoot a single horse. What about being alone and brave? You can cry all the way, but you can't be angry. You have to go through the days when nobody cares about it to welcome applause and flowers.

上面这个句子, 我们统计一下字符的数量, 同样为了方便, 我们只显示 TOP5 的字符

' ', 41
'a', 20
'o', 19
'e', 16
't', 14
...
...
...

这样一来, 是不是我用什么二进制代表什么字符对传输总量有着非常大的影响

用 0 代表’a’ == 1bit * 20 = 20bit
用 101 代表’a’ == 3bit * 20 = 60bit

哈夫曼树

哈夫曼编码就是解决这个问题的

利用变长编码, 对频率高的用占bit数少的编码, 对频率低的用占bit多的编码

所以我们如何才能构建这个编码呢? 需要两个信息, 字符和字符出现的频率.

这就涉及到哈夫曼树的生成

假使有这么一个数组[(‘ ‘, 41),(‘a’, 20),(‘o’, 19),(‘e’, 16),(‘t’, 14)]

算法是这样的

1. 从数组中取出频率最低的两个数据`('e', 16)`和`('t', 14)`

2. 将两个频率相加 16+14==30, 然后将衍生出来的数据, 放进数组里, 字符为`NULL`

[(' ', 41),('a', 20),('o', 19), (NULL, 30)]

接着重复1,2直到数组中的为空

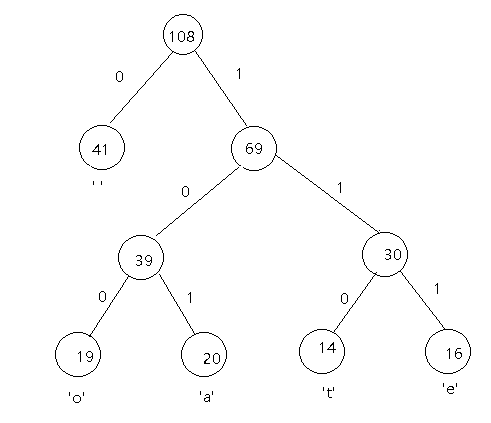
根据生成出来的二叉树, 我们可以得出结论.

叶子节点对应字符出现的频率(也就是权重)

' ' 这个字符出现41次, 用0编码(占用1bit)
'o' 这个字符出现19次, 用100编码(占用3bit)
'a' 这个字符出现20次, 用101编码(占用3bit)
't' 这个字符出现14次, 用110编码(占用3bit)
'e' 这个字符出现16次, 用111编码(占用3bit)

妙啊, 妙啊, 既减少了, 传输数据的总量, 又不会出现编码的冲突

这里总共传输的 bit 数是

1	1bit * 41 + 3bit * 19 + 3bit * 20 + 3bit * 14 + 3bit * 16 = 246bit

如果我们用等长编码(8bit)那么总共传输的 bit 数

1	8bit * 41 + 8bit * 19 + 8bit * 20 + 8bit * 14 + 8bit * 16 = 880bit

总结

变长编码, 能将减少传输数据的总量

哈夫曼编码, 能基于字符出现的频率进行不同长度的编码

保证在大量数据传输的过程中依然有较好的传输效率